1. 栈(stack)
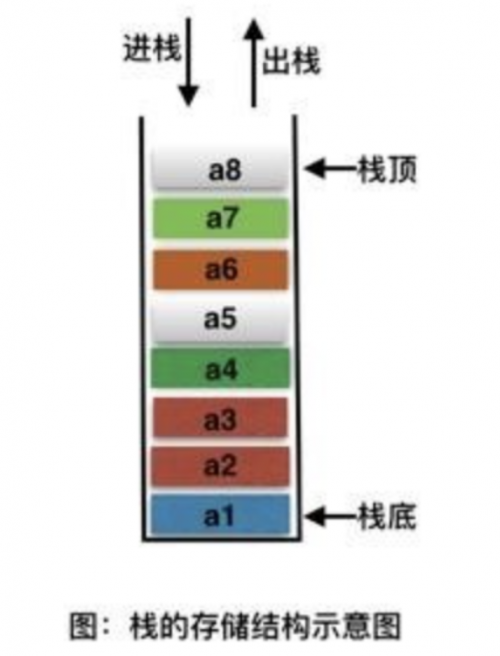
栈(stack)是限制插入和删除只能在一个位置上进行的表,该位置是表的末端,叫做栈顶(top)。它是后进先出(LIFO)的。对栈的基本操作只有 push(进栈)和 pop(出栈)两种,前者相当于插入,后者相当于删除最后的元素。
2. 队列(queue)
队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操作的端称为队尾,进行删除操作的端称为队头。
3. 链表(Link)
链表是一种数据结构,和数组同级。比如,Java 中我们使用的 ArrayList,其实现原理是数组。而LinkedList 的实现原理就是链表了。链表在进行循环遍历时效率不高,但是插入和删除时优势明显。
4. 散列表(Hash Table)
散列表(Hash table,也叫哈希表)是一种查找算法,与链表、树等算法不同的是,散列表算法在查找时不需要进行一系列和关键字(关键字是数据元素中某个数据项的值,用以标识一个数据元素)的比较操作。
散列表算法希望能尽量做到不经过任何比较,通过一次存取就能得到所查找的数据元素,因而必须要在数据元素的存储位置和它的关键字(可用key表示)之间建立一个确定的对应关系,使每个关键字和散列表中一个唯一的存储位置相对应。因此在查找时,只要根据这个对应关系找到给定关键字在散列表中的位置即可。这种对应关系被称为散列函数(可用 h(key)表示)。
用的构造散列函数的方法有:
(1)直接定址法: 取关键字或关键字的某个线性函数值为散列地址。
即:h(key) = key 或 h(key) = a * key + b,其中 a 和 b 为常数。
(2)数字分析法
(3)平方取值法: 取关键字平方后的中间几位为散列地址。
(4)折叠法:将关键字分割成位数相同的几部分,然后取这几部分的叠加和作为散列地址。
(5)除留余数法:取关键字被某个不大于散列表表长 m 的数 p 除后所得的余数为散列地址,即:h(key) = key MOD p p ≤ m
(6)随机数法:选择一个随机函数,取关键字的随机函数值为它的散列地址,即:h(key) = random(key)
5. 排序二叉树
首先如果普通二叉树每个节点满足:左子树所有节点值小于它的根节点值,且右子树所有节点值大于它的根节点值,则这样的二叉树就是排序二叉树。
5.1 插入操作
首先要从根节点开始往下找到自己要插入的位置(即新节点的父节点);具体流程是:新节点与当前节点比较,如果相同则表示已经存在且不能再重复插入;如果小于当前节点,则到左子树中寻找,如果左子树为空则当前节点为要找的父节点,新节点插入到当前节点的左子树即可;如果大于当前节点,则到右子树中寻找,如果右子树为空则当前节点为要找的父节点,新节点插入到当前节点的右子树即可。
5.2 删除操作
删除操作主要分为三种情况,即要删除的节点无子节点,要删除的节点只有一个子节点,要删除的节点有两个子节点。
对于要删除的节点无子节点可以直接删除,即让其父节点将该子节点置空即可。
对于要删除的节点只有一个子节点,则替换要删除的节点为其子节点。
对于要删除的节点有两个子节点,则首先找该节点的替换节点(即右子树中最小的节点),接着替换要删除的节点为替换节点,然后删除替换节点。
5.3 查询操作
查找操作的主要流程为:先和根节点比较,如果相同就返回,如果小于根节点则到左子树中递归查找,如果大于根节点则到右子树中递归查找。因此在排序二叉树中可以很容易获取最大(最右最深子节点)和最小(最左最深子节点)值。



















 京公网安备 11010802030320号
京公网安备 11010802030320号