在机器学习的优化问题中，梯度下降法和牛顿法是常用的两种凸函数求极值的方法，他们都是为了求得目标函数的近似解。在逻辑斯蒂回归模型的参数求解中，一般用改良的梯度下降法，也可以用牛顿法。由于两种方法有些相似，我特地拿来简单地对比一下。
1.梯度下降法
梯度下降法用来求解目标函数的极值。这个极值是给定模型给定数据之后在参数空间中搜索找到的。
迭代过程为：
梯度下降法更新参数的方式为目标函数在当前参数取值下的梯度值，前面再加上一个步长控制参数alpha。梯度下降法通常用一个三维图来展示，迭代过程就好像在不断地下坡，最终到达坡底。为了更形象地理解，也为了和牛顿法比较，这里我用一个二维图来表示：
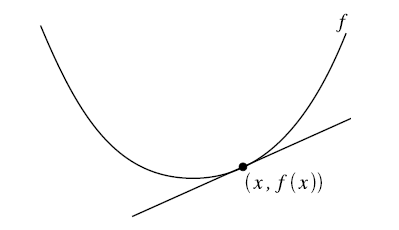
在二维图中，梯度就相当于凸函数切线的斜率，横坐标就是每次迭代的参数，纵坐标是目标函数的取值。
每次迭代的过程是这样：
首先计算目标函数在当前参数值的斜率(梯度)，然后乘以步长因子后带入更新公式，如图点所在位置(极值点右边)，此时斜率为正，那么更新参数后参数减小，更接近极小值对应的参数。
如果更新参数后，当前参数值仍然在极值点右边，那么继续上面更新，效果一样。
如果更新参数后，当前参数值到了极值点的左边，然后计算斜率会发现是负的，这样经过再一次更新后就会又向着极值点的方向更新。
根据这个过程我们发现，每一步走的距离在极值点附近非常重要，如果走的步子过大，容易在极值点附近震荡而无法收敛。解决办法：将alpha设定为随着迭代次数而不断减小的变量，但是也不能完全减为零。
2.牛顿法
首先得明确，牛顿法是为了求解函数值为零的时候变量的取值问题的，具体地，当要求解 f(θ)=0时，如果 f可导，那么可以通过迭代公式，来迭代求得最小值。
通过一组图来说明这个过程：
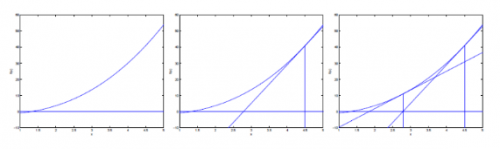
迭代的公式如下：
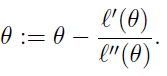
当θ是向量时，牛顿法可以使用下面式子表示：
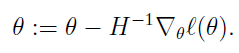
其中H叫做海森矩阵，其实就是目标函数对参数θ的二阶导数。
3.牛顿法和梯度下降法的比较
1.牛顿法：
是通过求解目标函数的一阶导数为0时的参数，进而求出目标函数最小值时的参数;
收敛速度很快;
海森矩阵的逆在迭代过程中不断减小，可以起到逐步减小步长的效果。
缺点：
海森矩阵的逆计算复杂，代价比较大，因此有了拟牛顿法。
2.梯度下降法：
是通过梯度方向和步长，直接求解目标函数的最小值时的参数;
越接近最优值时，步长应该不断减小，否则会在最优值附近来回震荡。
京公网安备 11010802030320号